
\(\lambda x.(M\ x)\ N \equiv_\beta M\ N\) whenever \(x \notin FV(M)\). 1 Note that, looking at β-equivalence, we have that Η is not always assumed (indeed, we will not assume it at the moment),īecause it has the consequence of making identity of λ-termsĮxtensional. \(\lambda x_ M\), provided that \(x\notin FV(M)\) We adopt at the outset a number of abbreviatory conventions. Parentheses, \(f(4)\), here both function and argument are within the Where function application is written with only the argument in Might have written like this: \(f(x) = M\). The term \(\lambda x.M\) represents a function, which we in high school Represents giving an argument ( N) to a function ( M). Represents a function, and an application (a term of the form \((M N)\))

The intuition is that an abstraction (a term of the form \(λ x.M\)) M\) is a λ term whenever x is a variable and \(M\) is a term
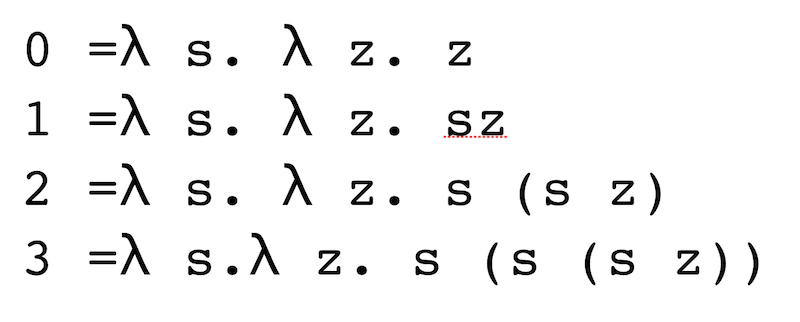
In the simplest version of the λ calculus a well-formed expression is called a (λ) term, and is defined by the following inductive definition: var a variable is a λ term app an application \((M N)\) is a λ term whenever both \(M\) and \(N\) are abs an abstraction \(\lambda x.

The λ calculus is a language for reasoning about functions. What follows is more than is relevant for the lecture, which onlyĭiscusses the material up to (but not including) the section Our first lecture is about the lambda calculus, which many of you are familiar with from your previous semantics course.


 0 kommentar(er)
0 kommentar(er)
